>立体構造変化・ダイナミックス
「生体分子の機能発現に必須である構造変化の原理を探る」
■背景 タンパク質やDNAなどの生体分子はアミノ酸や核酸が連なってできており、それらは美しい3次元の立体構造をしています(B-03,B-11,B-19)。そして、生物学的に重要な機能を発揮するときは、生体分子の構造は局所的に、もしくは大域的に変化します。よって、その構造変化を分子レベルでダイナミックに捉え、理解することが生命現象を考える上でもっとも基本的なことです。しかし、これは実験的にも理論・計算的にも難しい課題であり、現在研究者たちが様々なアプローチで研究を行っています。
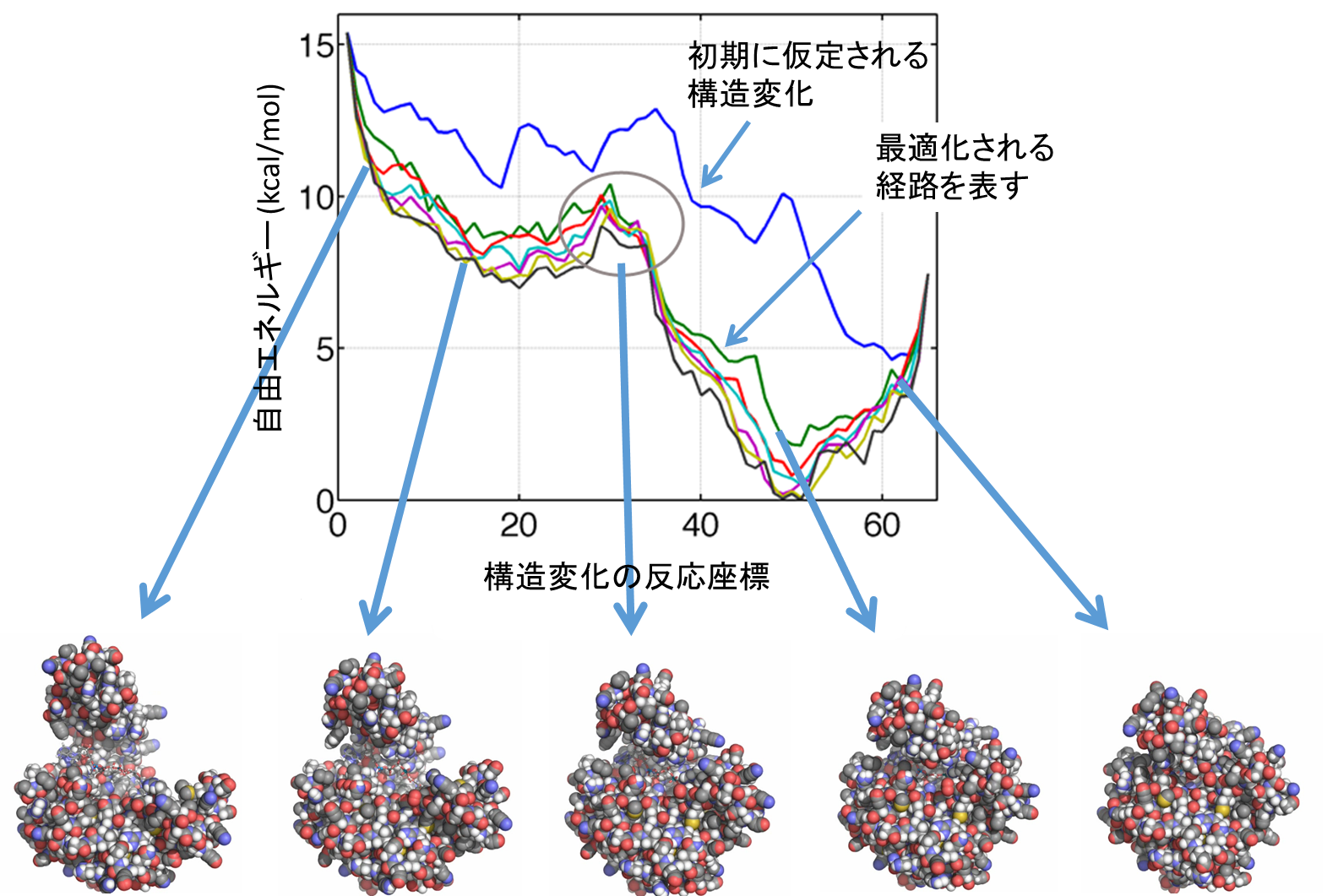
図1 酵素タンパク質の1つである、アデニル酸キナーゼの構造変化をストリング法で計算した例(下図)。左は開いた状態であり、右になるにつれて構造は閉じていく。このときは基質が挟まっており、基本的に右にいくにつれて自由エネルギーが小さくなっていく。上図は経路に沿って計算された自由エネルギーを表し、最初に仮定された経路から徐々に自由エネルギーが全体として下がっていき、最小自由エネルギー経路となる。文献2を改変して転載。
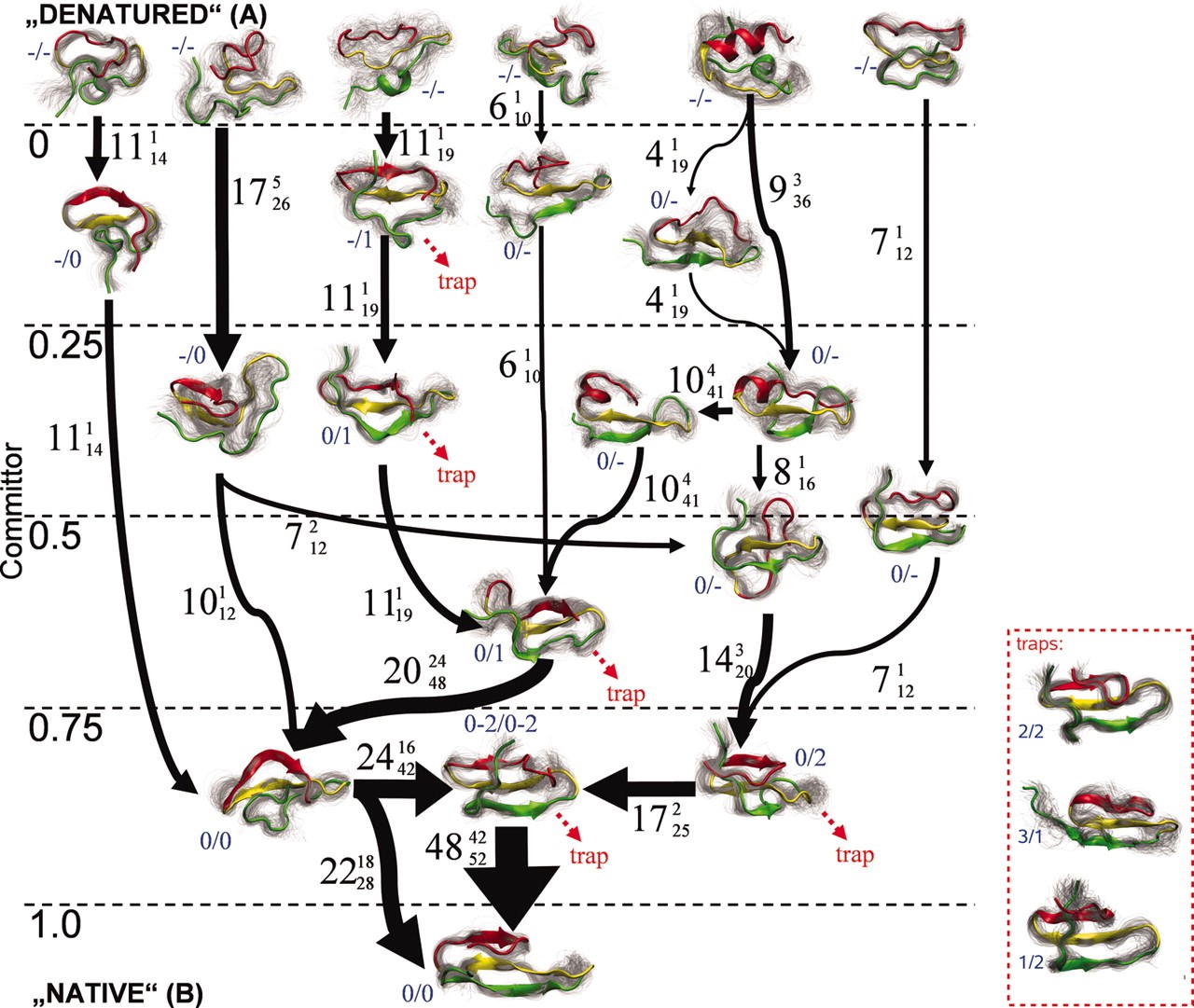
図2 マルコフ状態モデルによって、WWドメインのフォールディング経路を計算した例。状態はいくつかにクラスターでき、それらの間の遷移が観測される。太線は遷移パス理論によって計算される流束を表し、太いものほど大きい。また縦軸のcommittorはその場所から運動を始めたとして、最初にフォールドする確率を表す。文献3より転載。
■研究概要 ここでは理論・計算のアプローチについて述べます。生体分子の動きは、「経験的な力場」と呼ばれる原子に働く力の近似式を採用し、ニュートン方程式を解くことで精度よく記述できることが分かっています(分子動力学法と呼ばれますD-35, D-36, D-37)。しかし、構造変化のダイナミクスは非常に遅い、もしくは稀に起こるレアイベントであるため(文献1)、ニュートン方程式を単純に解くだけでは非常に時間がかかってしまいます。その理由は、ニュートン方程式を解くためには通常は逐次的な繰り返し計算をしており、それが計算のボトルネックになるからです。この問題を解決するために、現在では逐次的でない、並列計算を生かした計算アプローチがとられることが多くなっています。その一つはストリング法で、これは状態AからBへの構造変化の道筋を効率的に計算する手法です(図1, 文献2)。これは一つの軌道をいくつかに分割して、それぞれを並列に計算し、軌道に沿った自由エネルギーが最小になるような経路を探します。別の手法としては、マルコフ状態モデルがあります(図2, 文献3)。この手法では、反応座標の空間でばらばらになるように独立な分子動力学計算をしますが、そのデータを用いて状態間を遷移する離散的なモデルを作り上げます。その際に、1回の遷移で前にどこにいたかという情報を失うと仮定します(マルコフ性)。この手法を用いると、ある状態から遠い別の状態への遷移時間の分布などを求めることも可能になります。
■科学的・社会的意義 ここで紹介した手法や類似の手法によって、構造変化の反応経路やその反応レートが分かれば、構造変化のダイナミクスを分子レベルで詳細に理解することが可能になり、加えて実験との比較も容易になります。その結果として、細胞内のシグナリングや酵素反応、リガンド結合といった、生命現象に基本的な分子メカニズムを理解できるようになり、工学的な応用も開けることになります(E-04,E-05,E-14,E-15,E-19)。
■参考文献
1) Daniel M. Zuckerman 著, 藤崎弘士・藤崎百合共訳, 生体分子の統計力学入門 ―タンパク質の動きを理解するために―, 共立出版 (2014).
2) Y. Matsunaga, H. Fujisaki, T. Terada, T. Furuta, K. Moritsugu, and A. Kidera, Minimum Free Energy Path of Ligand-Induced Transition in Adenylate Kinase, PLoS Comput Biol 8(6): e1002555. doi:10.1371/journal.pcbi.1002555.
3) F. Noé, C. Schütte, E. Vanden-Eijnden, L. Reich, and T.R. Weikl, Constructing the equilibrium ensemble of folding pathways from short off-equilibrium simulations, Proc. Natl. Acad. Sci. USA 106, 19011-19016 (2009).
■良く使用する材料・機器
1) PCクラスター(HPCシステムズ)
2) グラフィックボードGPGPU (NVIDIA)
3) Amber, Gromacsなどの生体分子シミュレーションソフトウェア
 H28年度分野別専門委員
H28年度分野別専門委員
日本医科大学・物理学教室
藤崎弘士(ふじさきひろし)
https://nonad.zouri.jp/
「コンピュータの中でタンパク質が働くようすをみてみよう」
■背景 多くのタンパク質は形を変えることでいろいろな機能を果たします。コンピュータを使ったシミュレーションをおこなうと、その過程を原子のレベルで詳細に観察することができます。
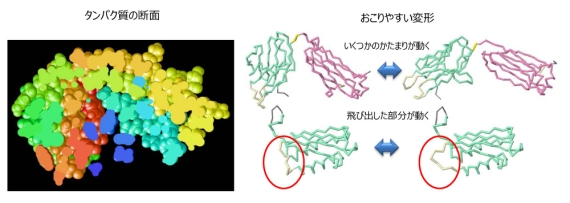
図1 タンパク質の断面(左)とおこりやすい変形(右)。
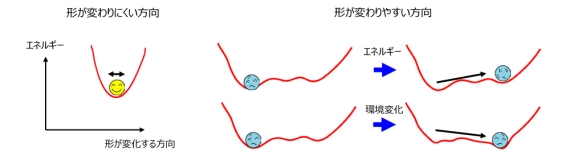
図2 タンパク質の変形とエネルギーの関係。
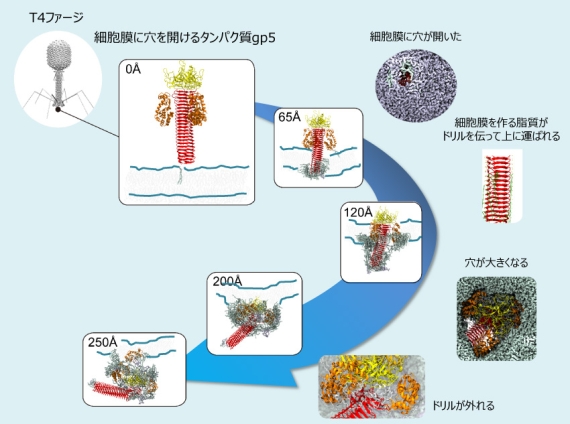
図3 コンピュータシミュレーションでみたT4ファージが細胞膜に穴を開ける過程。赤い部分が膜に穴を開けるドリルの役割を果たし、オレンジ色の部分は膜の内部を分解するリゾチームという酵素として働きます。
■研究概要
タンパク質は多数のアミノ酸が鎖状に連なってできていますが、その内部は図1左で示すように密に詰まっています。図1右はデータベース解析で見つかったタンパク質の典型的な変形を示しています(文献1)。例えば、緑で示したコンパクトなかたまりとピンクで示したかたまりの位置関係が変わるような変形や、外側に飛び出した部分(赤丸で囲った部分)が変形するような場合が多く見られます。タンパク質の内部は密につまっているので、内部の原子が単独で動こうとすると、周りと衝突してエネルギーが大きく上昇してしまうので、このようなことはほとんどおこりません(図2左)。一方、いくつかのかたまりが動くような変形や飛び出した部分の変形はエネルギーが大きく変わらないので、おこりやすいことになります(図2右)。エネルギー変化が小さいが構造の変化が大きな変形は、タンパク質が様々な機能を発揮する上で重要な役割を果たしています(文献2)。
T4ファージは大腸菌に感染して増殖するウイルスです。図3は、T4ファージが大腸菌に感染するために、先端についているタンパク質gp5を使って膜に穴をあける過程をコンピュータシミュレーションでみた結果です。gp5はドリルのように回転しながら膜に穴を開けます。本物のドリルのような全体の動きは一定ですが、gp5は変形しながら次々といろいろな仕事をします。まずドリルに当たる部分(赤い部分)が膜に穴を開けていきます。この部分は本物のドリルの溝のように、膜を形成する脂質分子を上に送っていく仕組みを持っています。オレンジ色の部分(リゾチーム)は膜に達すると、次第にドリルの部分から離れるとともに、穴を大きくしていきます。3つのリゾチームは周りからドリルを抱えているので、リゾチームが離れていくとドリルも外れます。その後、リゾチームは酵素として膜の内側を分解し、ウイルスが内部に侵入するのを助けます。このような過程は、実験で観察することができないので、コンピュータシミュレーションは重要な役割を果たします。
■科学的・社会的意義 コンピュータシミュレーションを使った研究は、タンパク質が生物のなかで様々な機能を発揮する仕組みを解明するために役立ちます。働く仕組みがわかるとタンパク質の機能を制御することにつながります。例えば、病気の治療や薬を開発するために役立つこともありますし、機能をもった新しい分子を設計するための指針も与えてくれます。
■参考文献
1)Nishima, W., G. Qi, S. Hayward, A. Kitao, (2006). “DTA: Dihedral transition analysis for characterization of the effects of large main-chain dihedral changes in proteins.” Bioinformatics, 25(5):.628-635.
2)Kitao, A., N. Go,(1999). “Investigating Protein Dynamics in Collective Coordinate Space.” Curr Opin Struct Biol, 9(2): 164-169.
3)Nishima, W., S. Kanamaru, F. Arisaka, A. Kitao, (2011). “Screw Motion Regulates Multiple Functions of T4 Phage Protein Gene Product 5 during Cell Puncturing.” J. Am. Chem. Soc., 133(34): 13571-13576.
■良く使用する材料・機器
1) 京コンピュータ(富士通)
2) スーパーコンピュータAltix(SGI)
3) スーパーコンピュータPRIMERGY(富士通)
4) PCクラスター(Dell)
5) グラフィックボードGPGPU(NVIDIA)
 H25年度分野別専門委員
H25年度分野別専門委員
東京大学・分子細胞生物学研究所
北尾彰朗 (きたおあきお)
https://www.iam.u-tokyo.ac.jp/MolDes/
